Category Archives: Code Generation

Code generation is a lot like compilation, except that the source isn’t a real programming language, and the target itself tends to be a high-level language.

Biology, Code Generation, fractals, Graphics, Technology

So You Feel Lucky?

May 13, 2014 Bill Leave a comment

I’ve just finished reading Stephen Jay Gould’s excellent book Wonderful Life (again) and it got me thinking about random trees.

In case you haven’t read it, Wonderful Life is about the fossil bed known as the Burgess Shales which contains extrordinarily well preserved fossils of soft and hard-bodied animals from a period just after the so-called Cambrian Explosion. The Cambrian Explosion marked the period when the seas first “exploded” with an enormous range of large, multicellular animals with hard shells that preserve easily. In the 1980s a detailed re-evaluation of the fossils found in the Burgess Shales provoked a scientific revolution in paleontology, because it turns out that only a small percentage of those fossils have any direct living descendants, and many of them represent previously unknown phyla (basic types of animals.) This did not fit comfortably with the established notion of evolution as ordered progress, with the basic groups of animals established early on and forming a predictable lineage all the way from microbe to man at the pinnacle. Rather it paints the picture of extinction being the norm, and the survival of one group or another very much in the hands of chance and historical contingency. The book is not an argument against Darwinism but rather a re-evaluation of some of its finer points. Crudely put, it’s not arguing against the existance of a Tree of Life, just questioning what shape the tree is.

Anyway with that in mind, and the somewhat vague hand-drawn trees in the book leaving my curiosity piqued, I started wondering what any real evolutionary tree might look like. Of course it’s impossible to ever produce an algorithm that will accurately represent a real evolutionary sequence, so I thought to keep it very simple.

We start with a “first progenitor“. It has two choices: form two new species or die out.

Each new species has the same option at the next toss of the coin. That’s it. In perl it would look something like this:

sub tree {
    my $tree = {};
    my @nodes = ($tree);
    while (@nodes) {
        my $node = shift @nodes;
        if (rand >= 0.5) {
            my $l = {};
            my $r = {};
            $node->{l} = $l;
            $node->{r} = $r;
            push @nodes, $l, $r;
        }
    }
}

sub tree {

my $tree = {};

my @nodes = ($tree);

while (@nodes) {

my $node = shift @nodes;

if (rand >= 0.5) {

my $l = {};

my $r = {};

$node->{l} = $l;

$node->{r} = $r;

push @nodes, $l, $r;

}

So there’s a 1/2 probability that the thing will never get started, and you’re left with a stump rather than a tree. But with 2 children, there’s only a ¼ chance that they will both die out, and if they both survive then there are 4 grandchildren, and so on. This code has a definite probability of running forever.

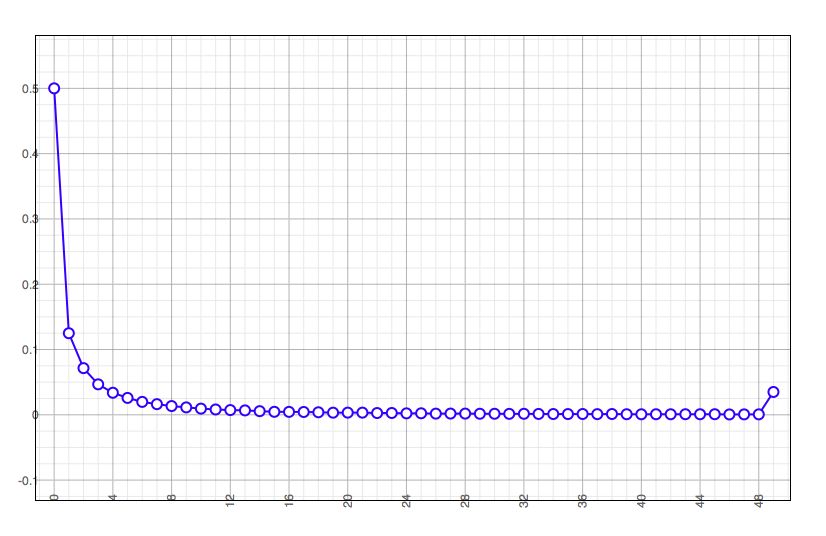
It turns out that if you run this a large number of times, and add up the number of each depth reached, you get a curve that asymptotically approaches zero at infinity:

The graph is normalized so the trees of depth zero come out at 0.5. The little kick at the right is those that reached the maximum depth in my test.

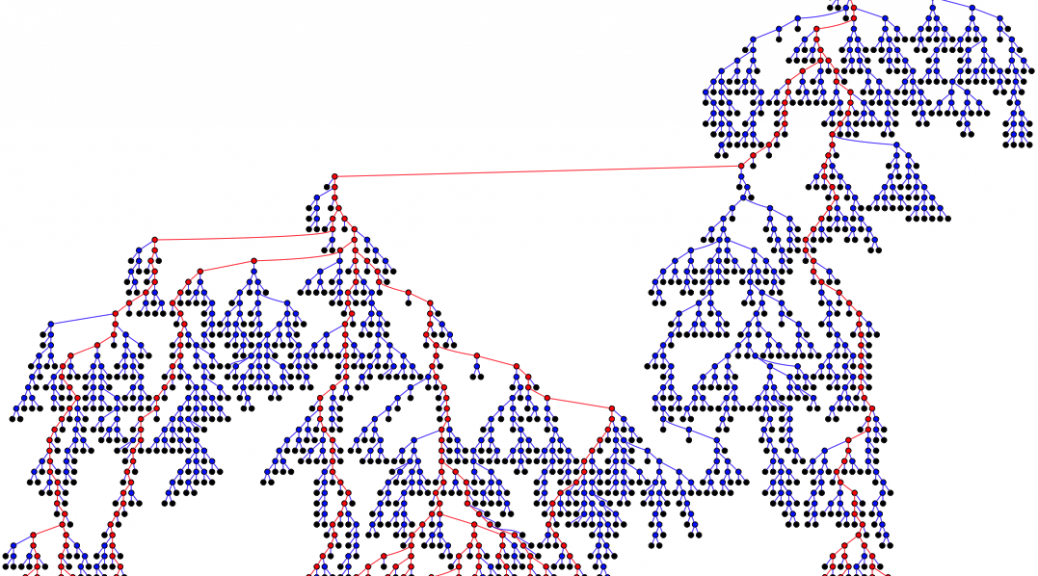
So what do these trees look like? I’ve given the game away by using a picture of one of them as the featured image for this post. As for generating the images, the excellent GraphViz comes to our rescue. With a little jiggery-pokery we can get the above perl code to produce a .dot file that we can feed to GraphViz and get a picture. I’ve extended the code to color nodes and vertices red if they are “survivors” (have descendents at the limiting depth) and black if they represent a species with no descendants. I’ve also changed the code to try again repeatedly until it generates a tree that reaches a limiting depth. Here’s a representative:

The limit was set at 60, so assuming 2 million years to create a species (I remember that figure from somewhere, I have a bad habit of throwing up unverified facts) this represents about 120,000,000 years of evolution from a single common ancestor. The interesting thing here I think is that the majority of branches don’t make it. Extinction is the norm, even for apparently large and flourishing branches. Apparently insignificant branches can suddenly flourish, and equally suddenly die out. I think this is close to Gould’s vision in general, if not in detail.

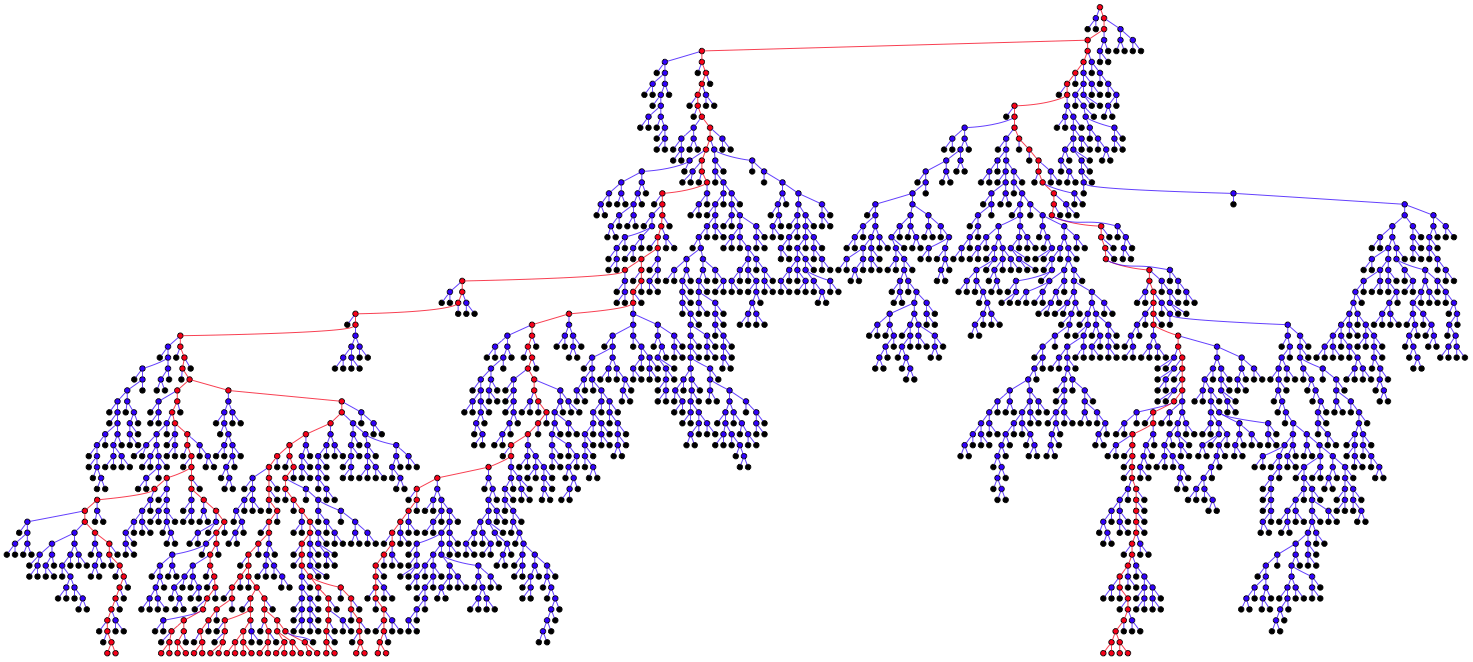
The other interesting thing is the huge variety of shapes. Some trees are wide, others are narrow, for example:

In this case all of the survivors share a common ancestor only a few generations (speciations) ago. This could easily be a model for the very earliest life, since the common ancestor of all current life on earth, who’s closest living relative is likely one of the Archaea, is far too complex to be a “first progenitor”.

I don’t know where I’m going with this from here, probably nowhere, but I think it’s interesting.

To finish off, here’s the full implementation of the tree generating code in case you want to try it yourself. You can pick up GraphViz from www.graphviz.org and run it from the command-line (the commands are called dot , neato , circo etc.) or via a gui.

#! /usr/bin/perl

use strict;
use warnings;
use Carp qw(confess);

use constant MAX => 50;

my $max = shift || MAX;

sub heads {
    return rand > 0.5;
}

sub iterate {
    my ($sub, @nodes) = @_;
    while (@nodes) {
        my $node = shift @nodes;
        push @nodes, $sub->($node);
    }
}

sub mark_ancestry {
    my ($node) = @_;
    while ($node) {
        return if $node->{survived};
        $node->{survived} = 1;
        $node = $node->{parent};
    }
}

sub free {
    my @nodes = @_;
    iterate(sub {
        my ($node) = @_;
        $node->{parent} = 0;
        return $node->{l} ? ($node->{l}, $node->{r}) : ();
    }, @nodes);
}

sub cull {
    my ($tree, $depth) = @_;
    iterate( sub {
        my ($node) = @_;
        if ($node->{depth} == $depth) {
            if ($node->{l}) {
                free($node->{l}, $node->{r});
                $node->{l} = $node->{r} = 0;
            }
            mark_ancestry($node);
        } elsif ($node->{l}) {
            return ($node->{l}, $node->{r});
        }
        return ();
    }, $tree);
}

sub make_tree {
    for (;;) {
        my $tree = {
            n => 0,
            live => 1,
            depth => 1,
            parent => 0
        };
        my @nodes = ($tree);
        my $n = 0;
        my $maxdepth = 0;

        while (@nodes) {
            my $node = shift @nodes;
            if ($node->{depth} == $max) {
                cull($tree, $max);
                return $tree;
            }
            if (heads) {
                my $l = {
                    n => ++$n,
                    depth => $node->{depth} + 1,
                    parent => $node,
                };
                my $r = {
                    n => ++$n,
                    depth => $node->{depth} + 1,
                    parent => $node,
                };
                $maxdepth = $node->{depth} > $maxdepth
                          ? $node->{depth}
                          : $maxdepth;
                $node->{l} = $l;
                $node->{r} = $r;
                push @nodes, $l, $r;
            }
            else {
                $node->{died} = 1;
            }
        }
        free($tree);
    }
}

sub print_tree {
    my ($tree) = @_;
    print "digraph G {\n";
    iterate(sub {
        my ($node) = @_;
        my $fillcolor = $node->{survived}
                      ? 'red'
                      : $node->{died} ? 'black'
                                      : 'blue';
        print '    N' . $node->{n}
            . qq' [label="", style="filled",'
            . qq' fillcolor="$fillcolor" shape="circle"];\n';
        if ($node->{l}) {
            my ($lcolor, $rcolor) = ('blue', 'blue');
            $lcolor = 'red' if $node->{l}{survived};
            $rcolor = 'red' if $node->{r}{survived};
            print '    N' . $node->{n}
                . ' -> N' . $node->{l}{n}
                . qq' [ color="$lcolor",'
                . qq' arrowhead="none" ];\n';
            print '    N' . $node->{n} . ' -> N'
                . $node->{r}{n}
                . qq' [ color="$rcolor",'
                . qq' arrowhead="none" ];\n';
            return ($node->{l}, $node->{r});
        }
        else {
            return ();
        }
    }, $tree);
    print "}\n";
}

print_tree(make_tree);

100

101

102

103

104

105

106

107

108

109

110

111

112

113

114

115

116

117

118

119

120

121

122

123

124

125

126

127

128

129

130

131

132

133

134

135

#! /usr/bin/perl

use strict;

use warnings;

use Carp qw(confess);

use constant MAX => 50;

my $max = shift || MAX;

sub heads {

return rand > 0.5;

}

sub iterate {

my ($sub, @nodes) = @_;

while (@nodes) {

my $node = shift @nodes;

push @nodes, $sub->($node);

}

sub mark_ancestry {

my ($node) = @_;

while ($node) {

return if $node->{survived};

$node->{survived} = 1;

$node = $node->{parent};

}

sub free {

my @nodes = @_;

iterate(sub {

my ($node) = @_;

$node->{parent} = 0;

return $node->{l} ? ($node->{l}, $node->{r}) : ();

}, @nodes);

}

sub cull {

my ($tree, $depth) = @_;

iterate( sub {

my ($node) = @_;

if ($node->{depth} == $depth) {

if ($node->{l}) {

free($node->{l}, $node->{r});

$node->{l} = $node->{r} = 0;

}

mark_ancestry($node);

} elsif ($node->{l}) {

return ($node->{l}, $node->{r});

}

return ();

}, $tree);

}

sub make_tree {

for (;;) {

my $tree = {

n => 0,

live => 1,

depth => 1,

parent => 0

};

my @nodes = ($tree);

my $n = 0;

my $maxdepth = 0;

while (@nodes) {

my $node = shift @nodes;

if ($node->{depth} == $max) {

cull($tree, $max);

return $tree;

}

if (heads) {

my $l = {

n => ++$n,

depth => $node->{depth} + 1,

parent => $node,

};

my $r = {

n => ++$n,

depth => $node->{depth} + 1,

parent => $node,

};

$maxdepth = $node->{depth} > $maxdepth

? $node->{depth}

: $maxdepth;

$node->{l} = $l;

$node->{r} = $r;

push @nodes, $l, $r;

}

else {

$node->{died} = 1;

}

free($tree);

}

sub print_tree {

my ($tree) = @_;

print "digraph G {\n";

iterate(sub {

my ($node) = @_;

my $fillcolor = $node->{survived}

? 'red'

: $node->{died} ? 'black'

: 'blue';

print ' N' . $node->{n}

. qq' [label="", style="filled",'

. qq' fillcolor="$fillcolor" shape="circle"];\n';

if ($node->{l}) {

my ($lcolor, $rcolor) = ('blue', 'blue');

$lcolor = 'red' if $node->{l}{survived};

$rcolor = 'red' if $node->{r}{survived};

print ' N' . $node->{n}

. ' -> N' . $node->{l}{n}

. qq' [ color="$lcolor",'

. qq' arrowhead="none" ];\n';

print ' N' . $node->{n} . ' -> N'

. $node->{r}{n}

. qq' [ color="$rcolor",'

. qq' arrowhead="none" ];\n';

return ($node->{l}, $node->{r});

}

else {

return ();

}

}, $tree);

print "}\n";

}

print_tree(make_tree);

Code Generation, Technology

A Slightly Non-Standard Application

February 16, 2014 Bill Leave a comment

Here’s an application of code generation that doesn’t fit the standard Enterprise Application mold: here I’m using code generation to build a class heirarchy for abstract syntax trees.

The idea is pretty simple. An abstract syntax tree is a tree containing the results of parsing a programming language. Nodes of the tree could be function calls, operator application or control flow constructs, and the leaves of the tree would be comstants and variables. Of course these trees cannot be constructed arbitrarily, it doesn’t often make sense to add an integer to a record for example, so the constructors for the nodes need to declare (or, in an untyped language, type-check) their arguments. Each node will furthermore need accessors and probably an accept() method for the Visitor pattern, so that is a substantial amount of boiler-plate code for something that is easily describeable at a very high level.

Here’s a snapshot of the AST definition from F♮:

abstract      Expr()
Expr          Char(scalar value) # [id]
Expr          Number(scalar value)

Expr          WildCard()

abstract Expr Symbol() # [id]
Symbol        DollarName(scalar name)
Symbol        Name(scalar name)
Symbol        TypeName(scalar name)

abstract Expr List()
List          Cons(Expr car, List cdr)
List          Nil()

abstract Expr Sequence()
Sequence      Statement(Expr car, Sequence cdr)
Sequence      EmptySequence()

abstract Expr Constructors()
Constructors  Constructor(Expr car, Constructors cdr)
Constructors  EmptyConstructor()

Expr          Typedef(Expr type, Constructors constructors)
Expr          Type(Expr type)

Expr          Apply(Expr op, List args)
Expr          End(Expr expr)
Expr          Define(Symbol name, Expr value)
Expr          Declare(Name name)
Expr          Lambda(List args, Sequence body)
Expr          LambdaSwitch(List lambdas)
Expr          Try(Apply attempt, LambdaSwitch catches)
Expr          Throw(List exprs)
Expr          String(scalar value)

Expr          LambdaLet(List formals, List actuals, Sequence Body)
Expr          LambdaSwitchLet(List actuals, List lambdas)

# these next are rewritten by the RewritingVisitor
Expr          And(Expr a, Expr b)
Expr          Or(Expr a, Expr b)
Expr          Not(Expr)
Expr          If(Expr test, Sequence consequent, Sequence alternative)
Expr          Then(Expr first, Expr second)
Expr          Pairs(List list)
Expr          Switch(List exprs, LambdaSwitch lambdas)

abstract Expr()

Expr Char(scalar value) # [id]

Expr Number(scalar value)

Expr WildCard()

abstract Expr Symbol() # [id]

Symbol DollarName(scalar name)

Symbol Name(scalar name)

Symbol TypeName(scalar name)

abstract Expr List()

List Cons(Expr car, List cdr)

List Nil()

abstract Expr Sequence()

Sequence Statement(Expr car, Sequence cdr)

Sequence EmptySequence()

abstract Expr Constructors()

Constructors Constructor(Expr car, Constructors cdr)

Constructors EmptyConstructor()

Expr Typedef(Expr type, Constructors constructors)

Expr Type(Expr type)

Expr Apply(Expr op, List args)

Expr End(Expr expr)

Expr Define(Symbol name, Expr value)

Expr Declare(Name name)

Expr Lambda(List args, Sequence body)

Expr LambdaSwitch(List lambdas)

Expr Try(Apply attempt, LambdaSwitch catches)

Expr Throw(List exprs)

Expr String(scalar value)

Expr LambdaLet(List formals, List actuals, Sequence Body)

Expr LambdaSwitchLet(List actuals, List lambdas)

# these next are rewritten by the RewritingVisitor

Expr And(Expr a, Expr b)

Expr Or(Expr a, Expr b)

Expr Not(Expr)

Expr If(Expr test, Sequence consequent, Sequence alternative)

Expr Then(Expr first, Expr second)

Expr Pairs(List list)

Expr Switch(List exprs, LambdaSwitch lambdas)

This is a high level but complete description of the required classes, all of the details of implementation are merely repetitive, which makes it a perfect candidate for code generation.

So, given this description, and a couple of command-line options to cover class prefixes etc., my treebuilder (tbd) will generate all of the classes required. For example, here’s the generated class definition for Expr If(Expr test, Sequence consequent, Sequence alternative):

# WARNING: Automatically generated from ast.tb on Sat May 29 18:51:18 2010 GMT. DO NOT EDIT! YOUR EDITS WILL BE LOST!

package Lang::FN::AST::If;
use strict;
use warnings;
use base qw(Lang::FN::AST::Expr);

=head1 NAME

Lang::FN::AST::If - a tree node, a type of Lang::FN::AST::Expr.

=head1 SYNOPSIS

  use Lang::FN::AST::API;
  my $if = If($test, $consequent, $alternative);

  my $test = $if->getTest();
  my $consequent = $if->getConsequent();
  my $alternative = $if->getAlternative();
  $if->accept(new Lang::FN::AST::Visitor());

=head1 METHODS

Individual Lang::FN::AST::If methods are described below.

=head2 new

  my $If = new Lang::FN::AST::If($test, $consequent, $alternative);

or better:

  use Lang::FN::AST::API;
  my $If = If($test, $consequent, $alternative);

The C<If()> subroutine is provided by
C<Lang::FN::AST::API> to make
it easier to create instances of C<Lang::FN::AST::If>.
In either case
C<$test>
must be a
C<Lang::FN::AST::Expr>, C<$consequent>
must be a
C<Lang::FN::AST::Sequence> and C<$alternative>
must be a
C<Lang::FN::AST::Sequence>.

=cut

sub new {
    die "wrong number of arguments to Lang::FN::AST::If::new(\$test, \$consequent, \$alternative)\n"
        unless @_ == 4;

    my ($class, $test, $consequent, $alternative) = @_;

    die "argument test to If is not a Lang::FN::AST::Expr, it is a ",
        (ref($test) || 'scalar'), "\n"
        unless defined($test)
               && $test->isa('Lang::FN::AST::Expr');
    die "argument consequent to If is not a Lang::FN::AST::Sequence, it is a ",
        (ref($consequent) || 'scalar'), "\n"
        unless defined($consequent)
               && $consequent->isa('Lang::FN::AST::Sequence');
    die "argument alternative to If is not a Lang::FN::AST::Sequence, it is a ",
        (ref($alternative) || 'scalar'), "\n"
        unless defined($alternative)
               && $alternative->isa('Lang::FN::AST::Sequence');

    return bless {
        _test => $test,
        _consequent => $consequent,
        _alternative => $alternative,
    }, $class;
}

=head2 getTest

  my $test = $If->getTest();

gets the value of the C<test> field,
which is a C<Lang::FN::AST::Expr>.

=cut

sub getTest {
    my ($self) = @_;
    return $self->{_test};
}

=head2 getConsequent

  my $consequent = $If->getConsequent();

gets the value of the C<consequent> field,
which is a C<Lang::FN::AST::Sequence>.

=cut

sub getConsequent {
    my ($self) = @_;
    return $self->{_consequent};
}

=head2 getAlternative

  my $alternative = $If->getAlternative();

gets the value of the C<alternative> field,
which is a C<Lang::FN::AST::Sequence>.

=cut

sub getAlternative {
    my ($self) = @_;
    return $self->{_alternative};
}

=head2 accept

  $If->accept(new Lang::FN::AST::Visitor());

Accepts a C<Lang::FN::AST::Visitor> and calls its C<visitIf>
method, passing it C<$self> (i.e. a C<Lang::FN::AST::If>) as argument.

=cut

sub accept {
    my ($self, $visitor) = @_;
    return $visitor->visitIf($self);
}

=head2 eq

   if ($If->eq($other)) {
       ...
   }

Returns true if the argument C<$other> is recursively equal to C<$self>.

=cut

sub eq {
    my ($self, $other) = @_;
    if (ref($other) eq 'Lang::FN::AST::If') {
        return 1
            && $self->getTest->eq($other->getTest)
            && $self->getConsequent->eq($other->getConsequent)
            && $self->getAlternative->eq($other->getAlternative)
    } else {
        return 0;
    }
}

=head2 isIf

Returns true.

=cut

sub isIf { 1 }

=head1 AUTHOR

Automatically generated from ast.tb on Sat May 29 18:51:18 2010 GMT.

=head1 SEE ALSO

The other generated node classes:
L<Lang::FN::AST::And>,
L<Lang::FN::AST::Apply>,
L<Lang::FN::AST::Char>,
L<Lang::FN::AST::Cons>,
L<Lang::FN::AST::Constructor>,
L<Lang::FN::AST::Constructors>,
L<Lang::FN::AST::Declare>,
L<Lang::FN::AST::Define>,
L<Lang::FN::AST::DollarName>,
L<Lang::FN::AST::EmptyConstructor>,
L<Lang::FN::AST::EmptySequence>,
L<Lang::FN::AST::End>,
L<Lang::FN::AST::Expr>,
L<Lang::FN::AST::Lambda>,
L<Lang::FN::AST::LambdaLet>,
L<Lang::FN::AST::LambdaSwitch>,
L<Lang::FN::AST::LambdaSwitchLet>,
L<Lang::FN::AST::List>,
L<Lang::FN::AST::Name>,
L<Lang::FN::AST::Nil>,
L<Lang::FN::AST::Not>,
L<Lang::FN::AST::Number>,
L<Lang::FN::AST::Or>,
L<Lang::FN::AST::Pairs>,
L<Lang::FN::AST::Sequence>,
L<Lang::FN::AST::Statement>,
L<Lang::FN::AST::String>,
L<Lang::FN::AST::Switch>,
L<Lang::FN::AST::Symbol>,
L<Lang::FN::AST::Then>,
L<Lang::FN::AST::Throw>,
L<Lang::FN::AST::Try>,
L<Lang::FN::AST::Type>,
L<Lang::FN::AST::TypeName>,
L<Lang::FN::AST::Typedef>,
L<Lang::FN::AST::WildCard>,
an abstract visitor that can be subclassed to walk them:
L<Lang::FN::AST::Visitor>,
and the API that makes them available: L<Lang::FN::AST::API>.

=cut

1;

100

101

102

103

104

105

106

107

108

109

110

111

112

113

114

115

116

117

118

119

120

121

122

123

124

125

126

127

128

129

130

131

132

133

134

135

136

137

138

139

140

141

142

143

144

145

146

147

148

149

150

151

152

153

154

155

156

157

158

159

160

161

162

163

164

165

166

167

168

169

170

171

172

173

174

175

176

177

178

179

180

181

182

183

184

185

186

187

188

189

190

191

192

193

194

195

196

197

198

199

200

201

202

203

204

205

206

207

208

209

210

# WARNING: Automatically generated from ast.tb on Sat May 29 18:51:18 2010 GMT. DO NOT EDIT! YOUR EDITS WILL BE LOST!

package Lang::FN::AST::If;

use strict;

use warnings;

use base qw(Lang::FN::AST::Expr);

=head1 NAME

Lang::FN::AST::If - a tree node, a type of Lang::FN::AST::Expr.

=head1 SYNOPSIS

use Lang::FN::AST::API;

my $if = If($test, $consequent, $alternative);

my $test = $if->getTest();

my $consequent = $if->getConsequent();

my $alternative = $if->getAlternative();

$if->accept(new Lang::FN::AST::Visitor());

=head1 METHODS

Individual Lang::FN::AST::If methods are described below.

=head2 new

my $If = new Lang::FN::AST::If($test, $consequent, $alternative);

or better:

use Lang::FN::AST::API;

my $If = If($test, $consequent, $alternative);

The C<If()> subroutine is provided by

C<Lang::FN::AST::API> to make

it easier to create instances of C<Lang::FN::AST::If>.

In either case

C<$test>

must be a

C<Lang::FN::AST::Expr>, C<$consequent>

must be a

C<Lang::FN::AST::Sequence> and C<$alternative>

must be a

C<Lang::FN::AST::Sequence>.

=cut

sub new {

die "wrong number of arguments to Lang::FN::AST::If::new(\$test, \$consequent, \$alternative)\n"

unless @_ == 4;

my ($class, $test, $consequent, $alternative) = @_;

die "argument test to If is not a Lang::FN::AST::Expr, it is a ",

(ref($test) || 'scalar'), "\n"

unless defined($test)

&& $test->isa('Lang::FN::AST::Expr');

die "argument consequent to If is not a Lang::FN::AST::Sequence, it is a ",

(ref($consequent) || 'scalar'), "\n"

unless defined($consequent)

&& $consequent->isa('Lang::FN::AST::Sequence');

die "argument alternative to If is not a Lang::FN::AST::Sequence, it is a ",

(ref($alternative) || 'scalar'), "\n"

unless defined($alternative)

&& $alternative->isa('Lang::FN::AST::Sequence');

return bless {

_test => $test,

_consequent => $consequent,

_alternative => $alternative,

}, $class;

}

=head2 getTest

my $test = $If->getTest();

gets the value of the C<test> field,

which is a C<Lang::FN::AST::Expr>.

=cut

sub getTest {

my ($self) = @_;

return $self->{_test};

}

=head2 getConsequent

my $consequent = $If->getConsequent();

gets the value of the C<consequent> field,

which is a C<Lang::FN::AST::Sequence>.

=cut

sub getConsequent {

my ($self) = @_;

return $self->{_consequent};

}

=head2 getAlternative

my $alternative = $If->getAlternative();

gets the value of the C<alternative> field,

which is a C<Lang::FN::AST::Sequence>.

=cut

sub getAlternative {

my ($self) = @_;

return $self->{_alternative};

}

=head2 accept

$If->accept(new Lang::FN::AST::Visitor());

Accepts a C<Lang::FN::AST::Visitor> and calls its C<visitIf>

method, passing it C<$self> (i.e. a C<Lang::FN::AST::If>) as argument.

=cut

sub accept {

my ($self, $visitor) = @_;

return $visitor->visitIf($self);

}

=head2 eq

if ($If->eq($other)) {

...

}

Returns true if the argument C<$other> is recursively equal to C<$self>.

=cut

sub eq {

my ($self, $other) = @_;

if (ref($other) eq 'Lang::FN::AST::If') {

return 1

&& $self->getTest->eq($other->getTest)

&& $self->getConsequent->eq($other->getConsequent)

&& $self->getAlternative->eq($other->getAlternative)

} else {

return 0;

}

=head2 isIf

Returns true.

=cut

sub isIf { 1 }

=head1 AUTHOR

Automatically generated from ast.tb on Sat May 29 18:51:18 2010 GMT.

=head1 SEE ALSO

The other generated node classes:

L<Lang::FN::AST::And>,

L<Lang::FN::AST::Apply>,

L<Lang::FN::AST::Char>,

L<Lang::FN::AST::Cons>,

L<Lang::FN::AST::Constructor>,

L<Lang::FN::AST::Constructors>,

L<Lang::FN::AST::Declare>,

L<Lang::FN::AST::Define>,

L<Lang::FN::AST::DollarName>,

L<Lang::FN::AST::EmptyConstructor>,

L<Lang::FN::AST::EmptySequence>,

L<Lang::FN::AST::End>,

L<Lang::FN::AST::Expr>,

L<Lang::FN::AST::Lambda>,

L<Lang::FN::AST::LambdaLet>,

L<Lang::FN::AST::LambdaSwitch>,

L<Lang::FN::AST::LambdaSwitchLet>,

L<Lang::FN::AST::List>,

L<Lang::FN::AST::Name>,

L<Lang::FN::AST::Nil>,

L<Lang::FN::AST::Not>,

L<Lang::FN::AST::Number>,

L<Lang::FN::AST::Or>,

L<Lang::FN::AST::Pairs>,

L<Lang::FN::AST::Sequence>,

L<Lang::FN::AST::Statement>,

L<Lang::FN::AST::String>,

L<Lang::FN::AST::Switch>,

L<Lang::FN::AST::Symbol>,

L<Lang::FN::AST::Then>,

L<Lang::FN::AST::Throw>,

L<Lang::FN::AST::Try>,

L<Lang::FN::AST::Type>,

L<Lang::FN::AST::TypeName>,

L<Lang::FN::AST::Typedef>,

L<Lang::FN::AST::WildCard>,

an abstract visitor that can be subclassed to walk them:

L<Lang::FN::AST::Visitor>,

and the API that makes them available: L<Lang::FN::AST::API>.

=cut

The point of all this is to be able to use these constructors directly in a yapp or similar grammar file. Here’s a snippet of these generated classes in action:

...
expr      :   int
          |   char
          |   string
...
          |   END expr %prec L_5 { End($_[2]) }
          |   expr '=' expr      { Apply(Name('='), Cons($_[1], Cons($_[3], Nil))) }
          |   expr THEN expr     { Then($_[1], $_[3]) }
          |   expr '&&' expr     { And($_[1], $_[3]) }
          |   expr '||' expr     { Or($_[1], $_[3]) }
          |   '!' expr           { Not($_[2]) }
          |   '(' expr ')'       { $_[2] }
...
          ;

ifexpr    :   IF '(' expr ')' block ELSE alternative
                            { If($_[3], $_[5], $_[7]) }
          ;

alternative : block
            | ifexpr
            ;

...

expr : int

| char

| string

...

| END expr %prec L_5 { End($_[2]) }

| expr '=' expr { Apply(Name('='), Cons($_[1], Cons($_[3], Nil))) }

| expr THEN expr { Then($_[1], $_[3]) }

| expr '&&' expr { And($_[1], $_[3]) }

| expr '||' expr { Or($_[1], $_[3]) }

| '!' expr { Not($_[2]) }

| '(' expr ')' { $_[2] }

...

;

ifexpr : IF '(' expr ')' block ELSE alternative

{ If($_[3], $_[5], $_[7]) }

;

alternative : block

| ifexpr

;

One of the visitors over the resulting tree is a rewriting visitor that converts some abstract syntax to simpler forms so that there are fewer constructs that need to be dealt with later on. Here’s the visitor routine that converts If abstract syntax to a function call:

sub visitIf {
    my ($self, $if) = @_;
    my $test = $if->getTest->accept($self);
    my $consequent = $if->getConsequent->accept($self);
    my $alternative = $if->getAlternative->accept($self);
    Apply(
        LambdaSwitch(
            Cons(
                Lambda(
                    Cons(TypeName('True'), Nil),
                    Statement(
                        End($consequent->getCar),
                        $consequent->getCdr
                    )
                ),
                Cons(
                    Lambda(
                        Cons(TypeName('False'), Nil),
                        $alternative
                    ),
                    Nil
                )
            )
        ),
        Cons($if->getTest->accept($self), Nil)
    )
}

sub visitIf {

my ($self, $if) = @_;

my $test = $if->getTest->accept($self);

my $consequent = $if->getConsequent->accept($self);

my $alternative = $if->getAlternative->accept($self);

Apply(

LambdaSwitch(

Cons(

Lambda(

Cons(TypeName('True'), Nil),

Statement(

End($consequent->getCar),

$consequent->getCdr

)

Cons(

Lambda(

Cons(TypeName('False'), Nil),

$alternative

Nil

)

Cons($if->getTest->accept($self), Nil)

)

}

Bill Hails

Category Archives: Code Generation

So You Feel Lucky?

A Slightly Non-Standard Application

Random Blogs